|
|
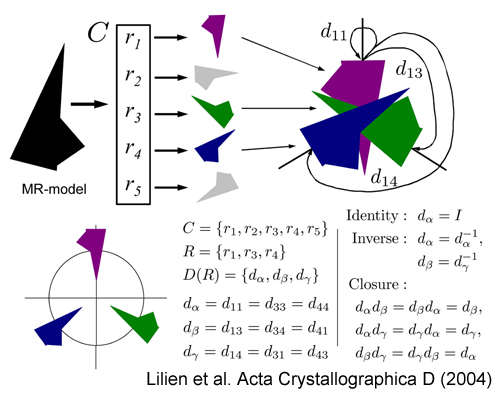
CRANS The core of the CRANS algorithm analyzes the set of rotation differences to identify finite sets of rotations that satisfy the subgroup axioms. Given a set of w cross-rotation peaks (rotations) C = {r1, r2, . . . , rw}, where ri is an element of the group of three-dimensional rotations SO(3), CRANS examines the w2 rotation differences dij where dij = ri−1 rj and ri−1 is the inverse of ri (such that ri−1 ri is the identity). Conceptually, the rotation difference dij is the rotation that rotates the model oriented by rj into the model oriented by ri (Figure). We can test the NCS consistency of a set of cross-rotation peaks by examining their rotation differences and verifying that they form a finite subgroup of SO(3). In the event of missing rotations, the CRANS algorithm completes each partial set of identified NCS-consistent rotations by generating missing rotations with quaternions. Although rotation differences can be computed using a number of rotation representations, we chose to use quaternions because they have a single compact representation with explicit axis and angle components, are easily composed, are free of singularities, and represent a uniform parameterization of rotation space. |